Competitive Programming: POJ 2663 – Tri Tiling

Description

In how many ways can you tile a 3xn rectangle with 2×1 dominoes?

Here is a sample tiling of a 3×12 rectangle.

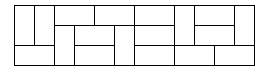
Input

Input consists of several test cases followed by a line containing -1. Each test case is a line containing an integer 0 <= n <= 30.

Output

For each test case, output one integer number giving the number of possible tilings.

Sample Input

2
8
12
-1

Sample Output

3
153
2131

Link to problem

Solution below . . .

Steps for Solving Dynamic Programming Problems

1. Define subproblems

Let be the number of tilings of a 3xN rectangle (which is what we’re looking for) and let denote the number of tilings of a 3xN rectangle with one of its corner squares removed.

********
********
********
  f(n)  

********  
********
 *******
  g(n)  

2. Write down the recurrence that relates subproblems

The recurrence functions are and . The functions can be illustrated as follows:

********   AA*******   AA******   A*******
******** = BB******* + B******* + A*******
********   CC*******   B*******   BB******
  f(n)   =  f(n-2)   +  g(n-1)  +  g(n-1)

********   A********   AA*******
******** = A******** + BB*******
 *******    ********    CC******
  g(n)   =   f(n-1)  +   g(n-2)

If you’re wondering why patterns like

AA*******
BC*******
BC*******

or

AB*******
AB*******
 CC******

are not represented, notice that they are subsets of existing patterns and thus already accounted for.

3. Recognize and solve the base cases

The base cases are: . (Re , there’s no way to remove the corner from a 3×0 rectangle.)

import java.util.Scanner;

public class Main {
	public static void main(String[] args) {

		Scanner sc = new Scanner(System.in);
				
		int n = sc.nextInt();
		
		while (n != -1) {
			
			// Optimization: If n is odd, the number of tilings = 0.
			if (n % 2 == 1) {
				System.out.println(0);
			}
			else {
				System.out.println(f(n));
			}
			
			n = sc.nextInt();
		}	
		sc.close();
	}

	private static int f(int n) {
		if (n == 0) return 1;
		if (n == 1) return 0;
		
		return f(n-2) + 2 * g(n-1);
	}

	private static int g(int n) {
		if (n < 2) return n;
		
		return f(n-1) + g(n-2);
	}
}