Competitive Programming: POJ 2074 – Line of Sight

Description

An architect is very proud of his new home and wants to be sure it can be seen by people passing by his property line along the street. The property contains various trees, shrubs, hedges, and other obstructions that may block the view. For the purpose of this problem, model the house, property line, and obstructions as straight lines parallel to the x axis:

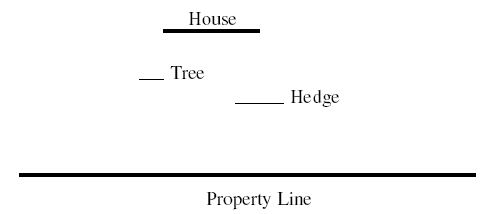
POJ 2074 - Line of Sight

Input

Because each object is a line, it is represented in the input file with a left and right x coordinate followed by a single y coordinate:

<x1> <x2> <y>

where x1, x2, and y are non-negative real numbers, x1 < x2 .

An input file can describe the architecture and landscape of multiple houses. For each house, the first line will have the coordinates of the house. The second line will contain the coordinates of the property line. The third line will have a single integer that represents the number of obstructions, and the following lines will have the coordinates of the obstructions, one per line.

Following the final house, a line “0 0 0” will end the file.

For each house, the house will be above the property line (house y > property line y). No obstruction will overlap with the house or property line, e.g. if obstacle y = house y, you are guaranteed the entire range obstacle[x1, x2] does not intersect with house[x1, x2].

Output

For each house, your program should print a line containing the length of the longest continuous segment of the property line from which the entire house can be to a precision of 2 decimal places. If there is no section of the property line where the entire house can be seen, print “No View”.

Sample Input

Sample Output

8.80
No View

Link to problem

Solution below . . .

Solution

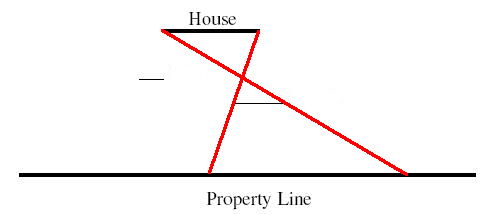
The key insight is that if we project lines from the endpoints of the house through the endpoints of an obstacle, the intersection of those lines with the property line form an interval, called a view in the code, within which the house is not entirely visible (see drawing below).

If we sort the views left to right, the largest gap between views is the answer we’re looking for.

Views

import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.Scanner;

public class Main {

  // compute intersection of line passing through a and b
  // with horizontal line at y
  static double ComputeLineIntersection(PT a, PT b, double y) {
    return (y - a.y) * (a.x - b.x) / (a.y - b.y) + a.x;
  }

  public static void main(String[] args) {

    Scanner sc = new Scanner(System.in);

    while (sc.hasNext()) {

      Line house = new Line();

      house.x1 = sc.nextDouble();
      house.x2 = sc.nextDouble();
      house.y = sc.nextDouble();

      if (house.empty())
        break;

      List<View> views = new ArrayList<View>();

      Line property = new Line();

      property.x1 = sc.nextDouble();
      property.x2 = sc.nextDouble();
      property.y = sc.nextDouble();

      int n = sc.nextInt();

      while (n-- > 0) {

        Line ob = new Line();

        ob.x1 = sc.nextDouble();
        ob.x2 = sc.nextDouble();
        ob.y = sc.nextDouble();

        // if obstacle is not between the house and the property
        // line, we can ignore it.
        if (ob.y >= house.y || ob.y <= property.y)
          continue;

        View v = new View();

        v.left = ComputeLineIntersection(new PT(house.x2, house.y),
            new PT(ob.x1, ob.y), property.y);
        v.right = ComputeLineIntersection(new PT(house.x1, house.y),
            new PT(ob.x2, ob.y), property.y);

        views.add(v);
      }

      Collections.sort(views);

      double max = 0;

      if (views.size() > 0) {
        if (views.get(0).left > property.x1)
          max = views.get(0).left - property.x1;
        if (views.get(0).right < property.x1)
          views.get(0).right = property.x1;
      }

      int rm; // the rightmost view so far
      int i;

      double tmp = 0;

      for (rm = 0, i = 1; i < views.size()
          && views.get(rm).right < property.x2; i++) {

        tmp = views.get(i).left - views.get(rm).right;
        if (tmp > 0) {

          rm = i;
          if (tmp > max)
            max = tmp;
        } else if (views.get(i).right > views.get(rm).right)
          rm = i;
      }

      if (views.size() > 0) {
        tmp = property.x2 - views.get(rm).right;
      } else {
        tmp = property.x2 - property.x1;
      }

      if (tmp > max)
        max = tmp;

      if (max > 0)
        System.out.printf("%.2fn", max);
      else
        System.out.println("No View");
    }
    sc.close();
  }
}


class PT {

  double x, y;

  PT(double x, double y) {
    this.x = x;
    this.y = y;
  }
}


class Line {

  double x1, x2;
  double y;

  boolean empty() {
    return x1 == 0 && x2 == 0 && y == 0;
  }
}


class View implements Comparable<View> {

  double left, right;

  @Override
  public int compareTo(View that) {
    return this.left - that.left <= 0 ? -1 : 1;
  }
}