Description
Your friend is a soccer fan and you were watching some World Cup matches with him. You liked this game, but the rules are very complicated for you, so you decided just to try to guess whether the given attack will end with a goal or not.
In the beginning, the ball is in the attacking team’s goalkeeper’s hands. On the attacking team, there’s a very talented goalscorer, who is waiting for his chance at the other end of the field. His teammates want to give him the ball so he can score. They can move the ball by passing it one to another along a straight line, but the defender can steal the pass if he is closer than d to the ball at any point throughout the pass. Now you want to know if the attacking team can score or not.
Formally, you are given the coordinates of all attacking players in an array attackingPlayers (where the player at index 0 is the goalkeeper and the player at the final index is the goalscorer), the coordinates of all defending players in an array defendingPlayers, and an integer d (representing how far each defending player can reach in order to intercept a pass). You need to find out whether it is possible to score a goal by passing the ball to the best scorer without any passes being intercepted.
Example
For attackingPlayers = [[0, 0], [1, 2], [3, 1]], defendingPlayers = [[2, 1]] and d = 1, the output should be canScore(attackingPlayers, defendingPlayers, d) = false.
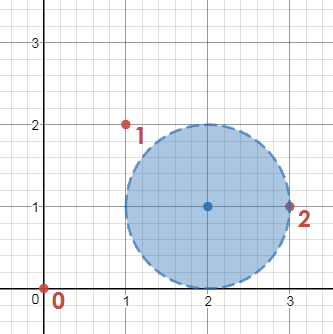
Attacking player 0 can pass to attacking player 1 without the pass being intercepted, but neither attacking player 0 nor attacking player 1 can pass to attacking player 2 (the goal scorer), so the goal cannot be completed.
For attackingPlayers = [[0, 0], [1, 2], [3, 3], [3, 1]], defendingPlayers = [[2, 1]] and d = 1, the output should be canScore(attackingPlayers, defendingPlayers, d) = true.
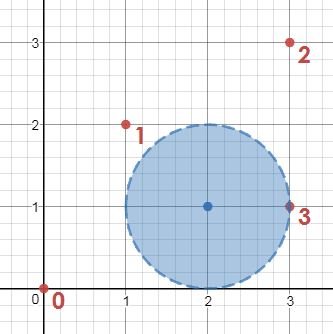
The goal can be scored if the ball is passed from attacking players 0 to 1 to 2 to 3.
For attackingPlayers = [[1, 2], [5, 3], [4, -2], [8, 0], [8, 6]], defendingPlayers = [[4, 4], [1, -1], [9, 2]] and d = 2, the output should be canScore(attackingPlayers, defendingPlayers, d) = true.
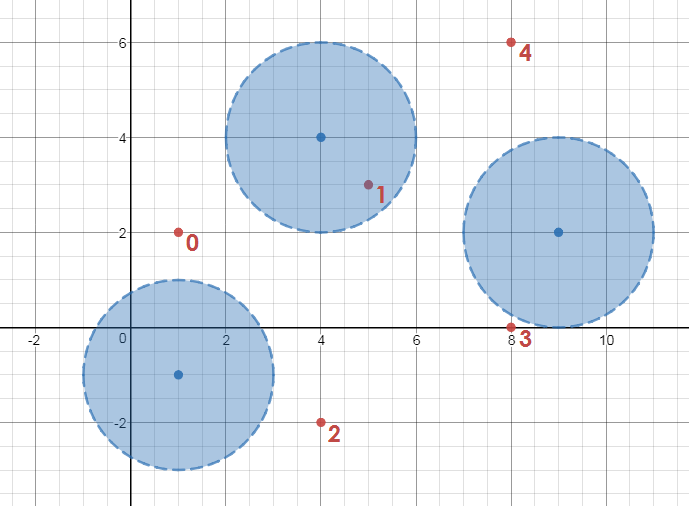
The goal can be scored if the ball is passed from attacking players 0 to 3 to 2 to 4.
Input/Output
- [execution time limit] 3 seconds (java)
- [input] array.array.integer attackingPlayers
An array of coordinates of all players from the attacking team. The first one is the goalkeeper’s coordinates and the last one is the best goalscorer’s coordinates.
Guaranteed constraints:
2 <= attackingPlayers.length <= 100
attackingPlayers[i].length = 2
104 <= attackingPlayers[i][j] <= 104 - [input] array.array.integer defendingPlayers
An array of coordinates of all players from the defending team.
Guaranteed constraints:
1 <= defendingPlayers.length <= 100
defendingPlayers[i].length = 2
-104 <= defendingPlayers[i][j] <= 104 - [input] integer d
The distance that each defending player can reach in intercepting a pass.
Guaranteed constraints:
0 <= d <= 104 - [output] boolean
Trueif attacking team can score a goal,Falseotherwise.
Solution below . . .
/* * We're going to create a graph with each attacking player as a vertex. * * For each pair of attacking players, we check each defensive player to * see if the defensive player is less than distance d from the line * segment between the attacking players. If no defensive player is close * enough to intercept a pass, we add an edge to the graph between the two * attacking players. * * Finally, we do a depth-first search from vertex 0 (the goalkeeper) to * find whether a path exists to the best scorer. * */ public class Main { static boolean[][] graph; static boolean[] marked; static boolean canScore(int[][] attackingPlayers, int[][] defendingPlayers, int d) { int apLen = attackingPlayers.length; int dpLen = defendingPlayers.length; graph = new boolean[apLen][apLen]; // check each pair of players for (int i = 0; i < apLen - 1; i++) { PT a = new PT(attackingPlayers[i][0], attackingPlayers[i][1]); for (int j = i + 1; j < apLen; j++) { PT b = new PT(attackingPlayers[j][0], attackingPlayers[j][1]); boolean ok = true; // is a defender within distance d? for (int k = 0; k < dpLen; k++) { PT c = new PT(defendingPlayers[k][0], defendingPlayers[k][1]); if (Geometry.DistancePointSegment(a, b, c) < d) { ok = false; break; } } // if defenders are too far, add the edge if (ok) { graph[i][j] = true; graph[j][i] = true; } } } marked = new boolean[apLen]; dfs(0); return marked[apLen - 1]; } static void dfs(int v) { marked[v] = true; for (int w = 0; w < graph[v].length; w++) { if (graph[v][w] && !marked[w]) { dfs(w); } } } public static void main(String[] args) { // Test cases // false // int[][] attackingPlayers = {{0, 0}, {1, 2}, {3, 1}}; // int[][] defendingPlayers = {{2, 1}}; // int d = 1; // true int[][] attackingPlayers = {{0, 0}, {1, 2}, {3, 3}, {3, 1}}; int[][] defendingPlayers = {{2, 1}}; int d = 1; System.out.println(canScore(attackingPlayers, defendingPlayers, d)); } } class Geometry { // Computational geometry functions static final double EPS = 1e-12; static double dot(PT p, PT q) { return p.x * q.x + p.y * q.y; } static double dist2(PT p, PT q) { return dot(p.subtract(q), p.subtract(q)); } static PT ProjectPointSegment(PT a, PT b, PT c) { double r = dot(b.subtract(a), b.subtract(a)); if (Math.abs(r) < EPS) return a; r = dot(c.subtract(a), b.subtract(a)) / r; if (r < 0) return a; if (r > 1) return b; return a.add(b.subtract(a).multiply(r)); } static double DistancePointSegment(PT a, PT b, PT c) { return Math.sqrt(dist2(c, ProjectPointSegment(a, b, c))); } } class PT { double x, y; PT() {} PT(double x, double y) { this.x = x; this.y = y; } PT(PT p) { this.x = p.x; this.y = p.y; { } } PT add(final PT p) { return new PT(x + p.x, y + p.y); } PT subtract(final PT p) { return new PT(x - p.x, y - p.y); } PT multiply(double c) { return new PT(x * c, y * c); } PT divide(double c) { return new PT(x / c, y / c); } @Override public String toString() { return "(" + x + "," + y + ")"; } }
