Competitive Programming: POJ 3281- Dining

Description

Cows are such finicky eaters. Each cow has a preference for certain foods and drinks, and she will consume no others.

Farmer John has cooked fabulous meals for his cows, but he forgot to check his menu against their preferences. Although he might not be able to stuff everybody, he wants to give a complete meal of both food and drink to as many cows as possible.

Farmer John has cooked F (1 <= F <= 100) types of foods and prepared D (1 <= D <= 100) types of drinks. Each of his N (1 <= N <= 100) cows has decided whether she is willing to eat a particular food or drink a particular drink. Farmer John must assign a food type and a drink type to each cow to maximize the number of cows who get both.

Each dish or drink can only be consumed by one cow (i.e., once food type 2 is assigned to a cow, no other cow can be assigned food type 2).

Input

Line 1: Three space-separated integers: N, F, and D

Lines 2..N+1: Each line i starts with a two integers Fi and Di, the number of dishes that cow i likes and the number of drinks that cow i likes. The next Fi integers denote the dishes that cow i will eat, and the Di integers following that denote the drinks that cow i will drink.

Output

Line 1: A single integer that is the maximum number of cows that can be fed both food and drink that conform to their wishes.

Sample Input

4 3 3
2 2 1 2 3 1
2 2 2 3 1 2
2 2 1 3 1 2
2 1 1 3 3

Sample Output

Hint

One way to satisfy three cows is:

Cow 1: no meal
Cow 2: Food #2, Drink #2
Cow 3: Food #1, Drink #1
Cow 4: Food #3, Drink #3

The pigeon-hole principle tells us we can do no better since there are only three kinds of food or drink. Other test data sets are more challenging, of course.

Link to problem

Solution below . . .

Let’s put the sample input in a table format so it’s easier to look at.

Cow	Food	Drink
1	{1,2}	{1,3}
2	{2,3}	{1,2}
3	{1,3}	{1,2}
4	{1,3}	{3}

This is a plain old max flow problem. We can use exactly the same Dinic class as the Secret Milking Machine problem. And again, Ford-Fulkerson or another max flow algorithm should work as well. The challenge is figuring out how to set up the network (see below). The capacity of all edges is 1.

Food, drink and cows

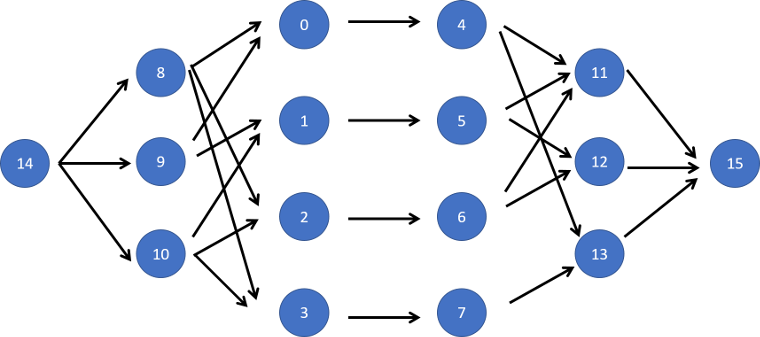
The program numbers the nodes like this: Cows first, then food, then drink, then start and end.

Numbered nodes

import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;

class Dinic {

  private final int MAXM = 25000;
  private final int MAXN = 25000;

  private int start, end;
  private int edgeCount = 0;

  private int[] head;
  private int[] vertex;
  private int[] next;
  private int[] capacity;
  private int[] flow;
  private int[] dist;
  private int[] curr;

  public Dinic() {
    head = new int[MAXN];
    Arrays.fill(head, -1);

    vertex = new int[MAXM];
    next = new int[MAXM];
    capacity = new int[MAXM];
    flow = new int[MAXM];

    dist = new int[MAXN];
    curr = new int[MAXN];
  }

  public void addEdge(int uu, int vv, int ca) {
    vertex[edgeCount] = vv;
    capacity[edgeCount] = ca;
    flow[edgeCount] = 0;
    next[edgeCount] = head[uu];
    head[uu] = edgeCount++;

    vertex[edgeCount] = uu;
    capacity[edgeCount] = 0;
    flow[edgeCount] = 0;
    next[edgeCount] = head[vv];
    head[vv] = edgeCount++;
  }

  private boolean bfs() {
    Arrays.fill(dist, -1);
    dist[start] = 0;

    Queue<Integer> qu = new LinkedList<Integer>();
    qu.add(start);

    while (!qu.isEmpty()) {
      int u = qu.poll();

      for (int e = head[u]; e != -1; e = next[e])
        if (dist[vertex[e]] == -1 && capacity[e] > flow[e]) {
          dist[vertex[e]] = dist[u] + 1;
          qu.add(vertex[e]);
        }
    }
    return dist[end] != -1;
  }

  private int dfs(int u, int a) {
    if (u == end || a == 0)
      return a;

    int f, Flow = 0;

    for (int e = curr[u]; e != -1; e = next[e]) {
      curr[u] = e;
      if (dist[vertex[e]] == dist[u] + 1
          && (f = dfs(vertex[e], Math.min(a, capacity[e] - flow[e]))) > 0) {
        flow[e] += f;
        flow[e ^ 1] -= f;
        Flow += f;
        a -= f;

        if (a == 0)
          break;
      }
    }
    return Flow;
  }

  public int maxflow(int start, int end) {
    this.start = start;
    this.end = end;

    int Flow = 0;

    while (bfs()) {
      curr = head.clone();
      Flow += dfs(start, Integer.MAX_VALUE);
    }
    return Flow;
  }
}

public class Main {

  public static void main(String[] args) {

    Scanner sc = new Scanner(System.in);

    int N = sc.nextInt();
    int F = sc.nextInt();
    int D = sc.nextInt();

    Dinic g = new Dinic();

    for (int i = 0; i < N; i++) {
      int fi = sc.nextInt();
      int di = sc.nextInt();

      for (int j = 0; j < fi; j++) {
        int f = sc.nextInt() - 1;
        g.addEdge(2 * N + f, i, 1);
      }

      g.addEdge(i, N + i, 1);

      for (int j = 0; j < di; j++) {
        int d = sc.nextInt() - 1;
        g.addEdge(N + i, 2 * N + F + d, 1);
      }
    }

    sc.close();
    
    int start = 2 * N + F + D;
    int end = 2 * N + F + D + 1;

    for (int i = 0; i < F; i++) {
      g.addEdge(start, 2 * N + i, 1);
    }
    for (int i = 0; i < D; i++) {
      g.addEdge(2 * N + F + i, end, 1);
    }

    System.out.println(g.maxflow(start,end));
  }
}